Recent work

The Mamoudou Gassama Affair

On May 26^th, 2018, it was reported in the French news that a four-year-old child fell from the 5^th floor's balcony of a building in Paris (France), and was able to catch the railing of the 4^th floor's balcony. An immigrant, Mamoudou Gassama, who was passing by decided to climb the building and rescued the child. Subsequently, Mamoudou was congratulated by French president, Emmanuel Macron, and was naturalized. In this study, by using kinematic equations and Newton's laws, it is shown that it is actually impossible for a four-year-old child (and probably for an adult too) to fall from a balcony and catch the railing of the lower balcony. This suggests that the rescue of the child could have been staged.

My Preprint where I present this study, arXiv:1807.05502 was noticed by famous French journalist, André Bercoff, who decided to give me an interview. The validity of my analysis was confirmed by several scientists, in particular by Florence Vivès who is a nuclear inspector at the United Nations. The interview (in French) is available below:

The superfluid density in continuous and discrete spaces: Avoiding misconceptions

It is well known that the superfluid density can be defined as the response of the free energy to a boundary phase-twist, which can be in turn related to the fluctuations of the winding number. However, what is much less well known is that such a definition is meaningful only for a particular class of Hamiltonians. Also, a given expression for the superfluid density that is valid for a cubic lattice cannot be directly applied to a different lattice geometry. In order to avoid these common mistakes, it is useful to go back to the experimental definition of a superfluid.

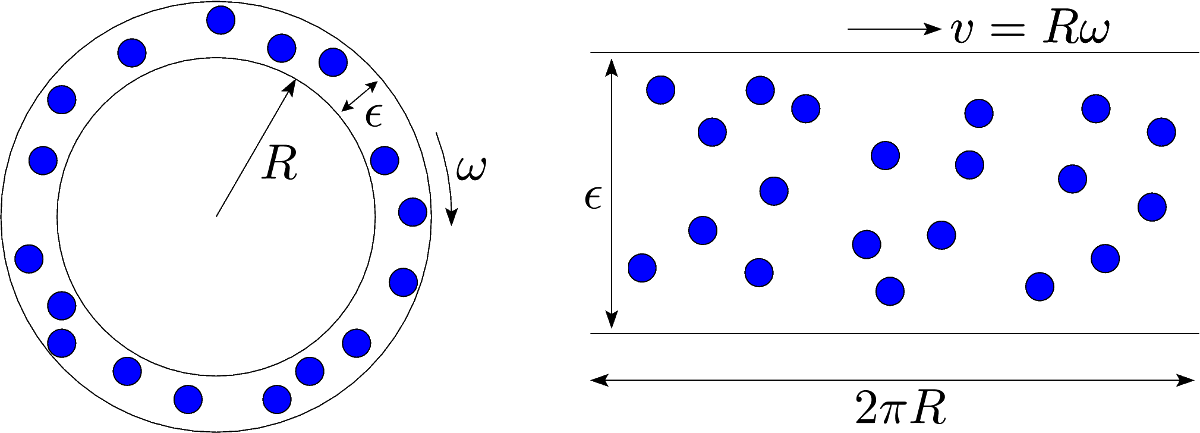
Experimentally, when a fluid is put into a slowly rotating torus, it can be observed that a part of the fluid (the superfluid) spontaneously decouples from the remaining fluid (the normal fluid) and comes to rest with respect to the lab frame when the temperature is lowered below some critical value. This experiment can be idealized by considering a “thought experiment” in which the fluid is placed between two rotating cylinders of radii R and R+ε. In the limit R>>ε, the system becomes equivalent to one enclosed between parallel planes moving at constant velocity and periodic along the velocity direction (see figure below). The outcome of this thought experiment is that, below some critical temperature, the superfluid decouples from the moving walls and comes to rest with respect to the lab frame.

The application of the Correspondence Principle to the momentum operator leads to a general expression for the superfluid density. For example, in the case of a continuous space isotropic Hamiltonian we get:

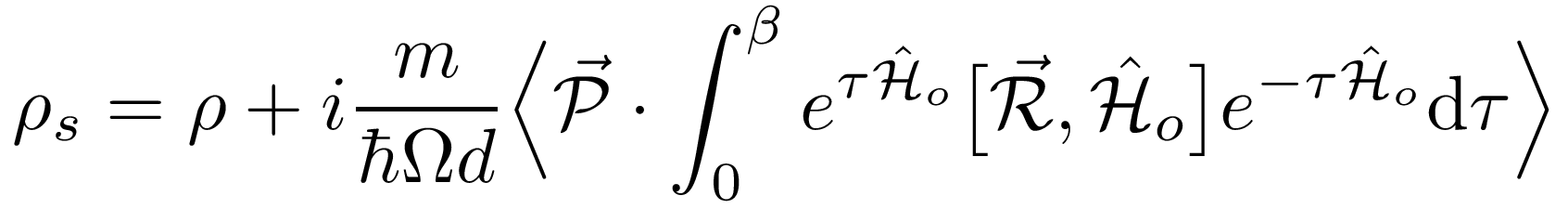
In the above expression, ρ is the total density, m is the mass of a particle, Ω is the d-dimensional volume of the system, P and R are the momentum and position operators, and H_o is the Hamiltonian. It can be shown that this expression is equal to the response of the free energy to a boundary phase twist only if the Hamiltonian satisfies the commutation relation:

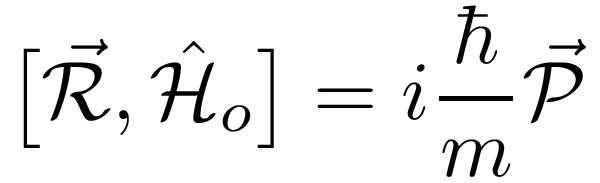
If this relation is not satisfied, then the above expression for ρ_s must be used. This expression can be measured exactly by using path-integral methods, such as the SGF algorithm.

For lattices, a given expression of the superfluid density that is valid for a cubic lattice needs to be modified in order to be applicable to a different lattice geometry. This is because the expression of the Laplacian in the natural coordinates of the lattice is associated to a pre-factor that introduces a change of the energy scale that needs to be reflected in the expression of the superfluid density. Also, the metric tensor depends on the choice of the basis and needs to be taken into account.

Consider for example a pyrochlore lattice, where the underlying Bravais lattice is face-centered cubic:

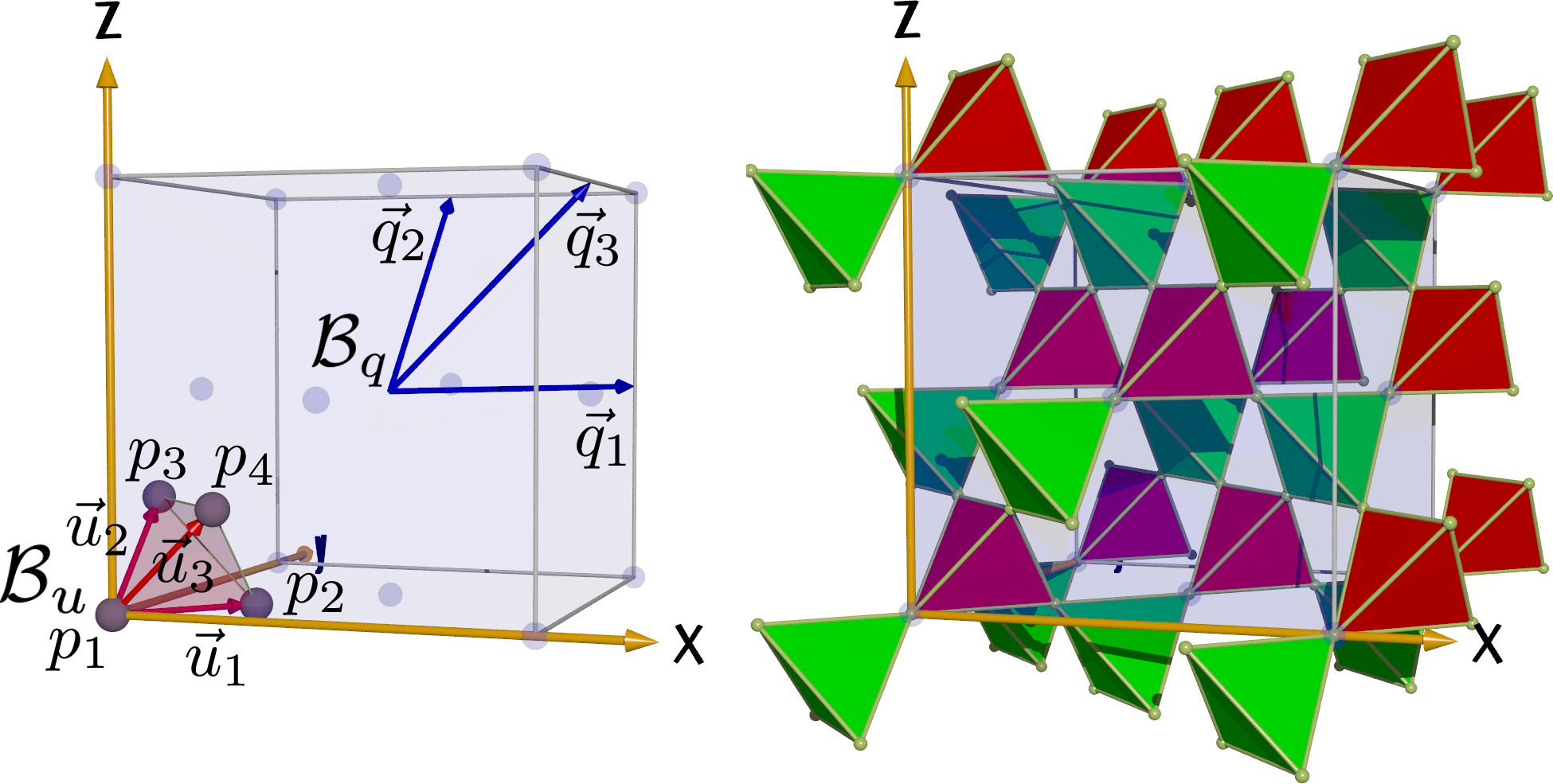
For a Hamiltonian of the form H=T+V, where T is the kinetic energy and V is any potential that is diagonal in the direct space, it can be shown that the dimensionless superfluid density takes the form

,

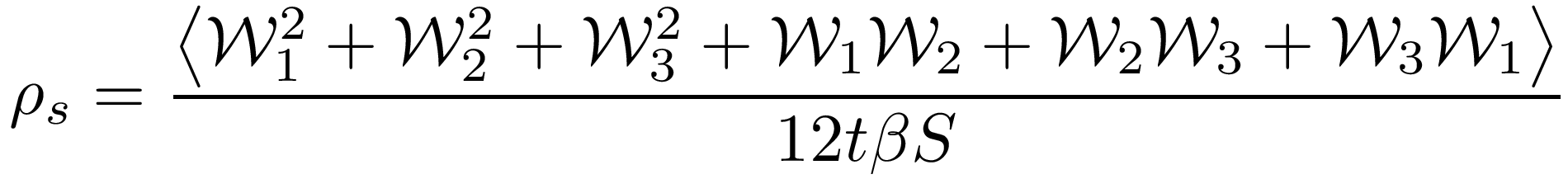where W_i are the components of the winding number along the primitive vectors of the underlying Bravais lattice, t is the hopping parameter, and S is the linear size of the lattice (counting primitive cells).

For more details, see Phys. Rev. B 90, 134503 (2014).

The Boson-Hubbard Model on a Kagome Lattice with Sextic Ring-Exchange Terms

Interest in ring-exchange interactions in quantum many-body systems has a long history originating from the study of quantum solids, a typical example is solid Helium-3. Recently the study of ring-exchange interactions has resurged with boson and spin models. In particular, multiple particle exchange has been suggested as a possible candidate to induce a normal “Bose metal” or “Bose liquid” phase at zero temperature, in which there are no broken symmetries associated with superfluidity or charge density wave phases. Studies on a square lattice with four-site ring-exchange plaquettes suggest that ordered phases always dominate. However, these results still leave the possibility that a Bose liquid or spin liquid phase may exist in certain frustrated lattices.

The model we consider in this work consists of hard-core bosons on a two-dimensional kagome lattice (figure below). A kinetic term t allows the particles to hop between first-neighboring sites. In addition, a sextic ring-exchange term K performs a correlated hopping of three particles within the same hexagon.

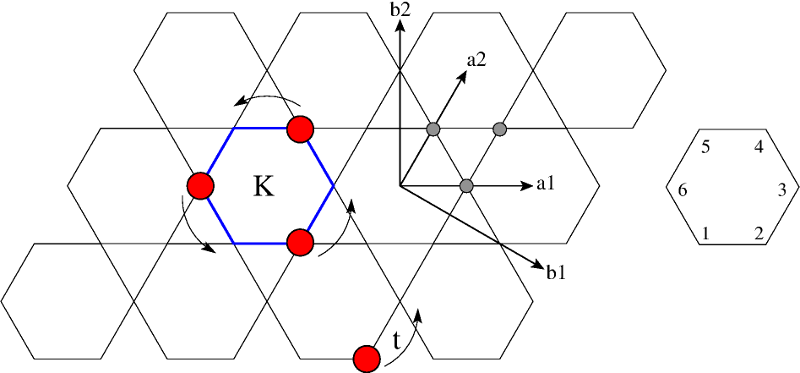
The Hamiltonian takes the form:

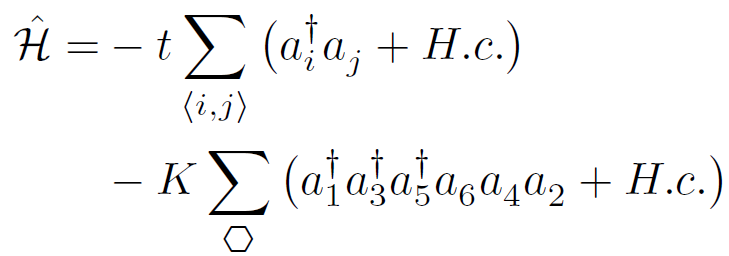
Since the sextic ring-exchange term couples six different sites at a time, an analytical treatment of the above Hamiltonian is rather complicated. On the other hand, the usual quantum Monte Carlo methods used in the studies on a square lattice need to decompose the Hamiltonian as a sum of two-site coupling terms, which is not possible in our case. These methods need such decomposition because they use a loop update that consists of building a closed path in space and imaginary time, and raising or lowering the occupation number of the sites that are visited. By construction these loops can update only one or two sites at a time, and are therefore suitable only for one-site or two-site coupling terms. However, the Stochastic Green Function (SGF) algorithm does not make use of such loop updates, instead, it performs a direct sampling of the partition function by distributing Hamiltonian terms randomly in space and imaginary time. No particular decomposition of the Hamiltonian is required. Therefore the update procedure is totally independent of the structure of the Hamiltonian, and can be applied to any n-site coupling term with efficiency. In this work, we use the SGF algorithm with fast updates and perform simulations of systems with sizes up to 18 × 18 hexagons (972 sites).

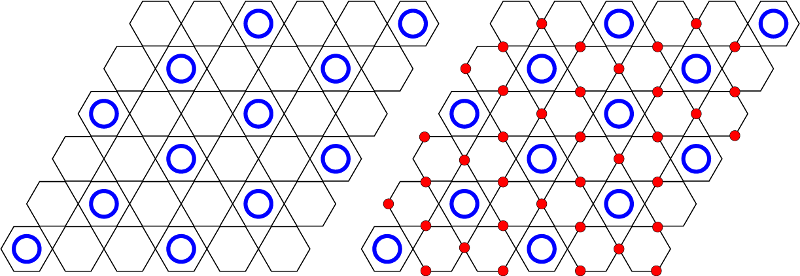
Instead of the expected Bose liquid phase, our simulations show that the system becomes unstable for large ring-exchange interactions and undergoes a phase separation, except at densities ρ=1/3 and ρ=2/3 for which the superfluid density vanishes and an incompressible state appears. When K is large, we expect the ground state to be formed by configurations that maximize the number of resonating hexagons. Because a resonance can occur only if the hexagon contains exactly three non-first-neighboring particles, it is not possible to have two resonating neighboring hexagons at first order in K. This suggests that a phase with a maximum number of resonating hexagons can be formed at ρ=1/3 by having all resonating hexagons surrounded by empty hexagons (figure below, left), or at ρ=2/3 by having all resonating hexagons surrounded by hexagons that contain three localized particles on the vertices of the triangles that are not shared with the resonating hexagons. (figure below, right). These phases can be understood as a form of valence bond solid in which each valence bond now involves six sites, in contrast with the usual two-site singlets.

This scenario is confirmed by looking at the structure factor. The figure below shows the structure factor S(k) for ρ=1/3, K=0, K=5t, and K=15t. For K=0 (left panel), only lattice Bragg peaks arise and correspond to the minima of the intensity (black and blue). For K=5t (middle panel), high intensity regions (red and yellow) appear in the center of triangles formed by the Bragg peaks. In the insulating phase, K=15t (right panel), the high intensity regions become localized at k_max=(2/3,1/3) in the (b₁,b₂) basis (and symmetry related momenta), and form a honeycomb lattice. Since k_max is parallel to a₁ and ||k_max||=4π, the phase has features that appear with a spatial frequency of 2/3 in the a₁ direction, in agreement with the suggested solid phase.

For more details, see Phys. Rev. B 87, 075146 (2013).